Nonlinear Mathematical Analysis based on an Insulin-Pancreatic Cells Model in the Presence of Epinephrine
DOI:
https://doi.org/10.17488/RMIB.45.1.2Keywords:
diabetes, model, β cells, LCISAbstract
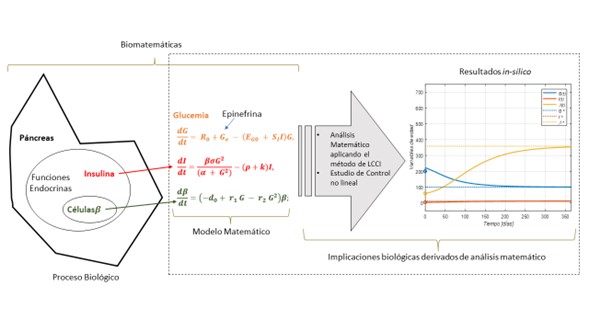
In this work, a nonlinear model is studied based on ordinary differential equations that describe the relationship between the mass of cells and the secretion of epinephrine. It analyzes the impact of stress associated with the cause of increased blood pressure and glucose levels in the body. The mathematical analysis is based on the appliance of the nonlinear control theory to define the maximum load capacity for each state variable, establishing a bounded positive invariant domain through the Localization of Compact Invariants Sets (LCIS) method. The objective is to determine the effects of epinephrine secretion on the increase of blood glucose levels; therefore, this analysis's results define the necessary and sufficient conditions in which epinephrine raises insulin and glucose levels in the presence of cells. The interest in studying this type of disease focuses on searching for a treatment or an analysis that guarantees complete control of glucose levels. This work's development and mathematical analysis strengthen current research on insulin-dependent diabetes mellitus around critical epinephrine factors that imply an increase in glucose in the body.
Downloads
References
A. Basto-Abreu, N. López-Olmedo, R. Rojas-Martínez, C. A. Aguilar-Salinas, et al., “Prevalencia de prediabetes y diabetes en México: Ensanut 2022,” Salud Publica Mex, vol. 65, pp. s163-s168, jun. 2023, doi: https://doi.org/10.21149/14832
I. I. Mohammed, I. Adamu, S. J. Barka, “Mathematical model for the dynamics of glucose, insulin and β-cell mass under the effect of trauma, excitement and stress,” Model. Numer. Simul. Mater. Sci., vol. 9, no. 4, pp. 71–96, oct. 2019, doi: https://doi.org/10.4236/mnsms.2019.94005
O. A. Montesinos-López, C. M. Hernández-Suarez, “Modelos matemáticos para enfermedades infecciosas,” Salud Publica Mex., vol. 49, no. 3, pp. 218–226, jul. 2007. [En línea]. Disponible en: https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0036-36342007000300007
E. F. Panqueba Moreno, J. M. Ruiz Vera, “Control óptimo de la glucosa en la sangre mediante infusión continua de insulina,” Ciencia Desarro., vol. 13, no. 2, pp. 49-67, jul. 2022, doi: https://doi.org/10.19053/01217488.v13.n2.2022.14173
F. X. Méndez-Carrillo, M. Beléndez-Vázquez, “Variables emocionales implicadas en el control de la diabetes: estrategias de intervención,” An. Psicol., vol. 10, no. 2, pp. 189–198, 1994. [En línea]. Disponible: https://revistas.um.es/analesps/article/view/29671
M. Zahedi, S. Kordrostami, M. Kalantarhormozi, M. Bagheri, “A Review of Hyperglycemia in COVID-19,” Cureus, vol. 15, no. 4, pp. 1-7, 2023, doi: https://doi.org/10.7759/cureus.37487
M. Sirlanci, M. E. Levine, C. C. Low Wang, D. J. Albers, A. M. Stuart, “A simple modeling framework for prediction in the human glucose–insulin system,” Chaos, vol. 33, no. 7, art. no. 073150, jul. 2023, doi: https://doi.org/10.1063/5.0146808
S. V. K. R. Rajeswari, P. Vijayakumar, “Mathematical Approaches in the Study of Diabetes Mellitus,” in Computer Vision and Robotics. Algorithms for Intelligent Systems, Lucknow, India, 2023, pp. 229-248, doi: https://doi.org/10.1007/978-981-19-7892-0_18
J. M. Munoz-Pacheco, C. Posadas-Castillo, E. Zambrano-Serrano, “The effect of a non-local fractional operator in an asymmetrical glucose-insulin regulatory system: Analysis, synchronization and electronic implementation,” Symmetry, vol. 12, no. 9, art. no. 1395, 2023, doi: https://doi.org/10.3390/sym12091395
B. Topp, K. Promislow, G. DeVries, R. M. Miura, D. T. Finegood, “A model of β-cell mass, insulin, and glucose kinetics: pathways to diabetes,” J. Theor. Biol., vol. 206, no. 4, pp. 605–619, oct. 2000, doi: https://doi.org/10.1006/jtbi.2000.2150
D. Laurent, K. F. Petersen, R. R. Russell, G. W. Cline, G. I. Shulman, “Effect of epinephrine on muscle glycogenolysis and insulin-stimulated muscle glycogen synthesis in human,” Am. J. Physiol., vol. 274, no. 1, pp. 130–138, 1998, doi: https://doi.org/10.1152/ajpendo.1998.274.1.E130
D. C. Deibert, R. A. Defronzo, “Epinephrine-induced insulin resistance in man,” J. Clin. Invest., vol. 65, no. 3, pp. 717–721, 1980, doi: https://doi.org/10.1172/JCI109718
A. P. Krishchenko, “Localization of Invariant Compact Sets of Dynamical Systems,” Differ. Equ., vol. 41, no. 12, pp. 1669–1676, 2005, doi: https://doi.org/10.1007/s10625-006-0003-6
D. Gamboa, C. E. Vázquez, P. J. Campos, “Nonlinear Analysis for a Type-1 Diabetes Model with Focus on T-Cells and Pancreatic β-Cells Behavior,” Math. Comput. Appl., vol. 25, no. 2, pp. 23, 2020, doi: https://doi.org/10.3390/mca25020023
D. Gamboa, C. E. Vázquez-López, R. Gutierrez, P. J. Campos, “Nonlinear Analysis of the C-Peptide Variable Related to Type 1-Diabetes Mellitus,” Symmetry, vol. 13, no. 7, pp. 1238, 2021, doi: https://doi.org/10.3390/sym13071238
D. Gamboa, L. N. Coria, P. A. Valle, “Ultimate Bounds for a Diabetes Mathematical Model Considering Glucose Homeostasis,” Axioms, vol. 11, no. 7, art. no. 320, 2022, doi: https://doi.org/10.3390/axioms11070320
A. P. Krishchenko, K. E. Starkov, “Localization of compact invariant sets of the Lorenz system,” Phys. Lett. A, vol. 353, no. 5, pp. 383-388, 2006, doi: https://doi.org/10.1016/j.physleta.2005.12.104
K. E. Starkov, “On dynamic tumor eradication conditions under combined chemical/anti-angiogenic therapies,” Phys. Lett. A, vol. 382, no. 6, pp. 387-393, 2018, doi: https://doi.org/10.1016/j.physleta.2017.12.025
K. Saranya, T. Iswarya, V. Mohan, K. E. Sathappan, L. Rajendran, “Mathematical modeling of Glucose, Insulin, β-Cell Mass: Homotopy Perturbation Method Approach,” Eur. J. Mol. Clin. Med., vol. 07, no. 02, pp. 3513–3530, 2020. [En línea]. Disponible en: https://ejmcm.com/uploads/paper/ca3ad85a4a3175b4f8ac48ac1f80300c.pdf
P. G. Jacobs, P. Herrero, A. Facchinetti, J. Vehi, et al., “Artificial intelligence and machine learning for improving glycemic control in diabetes: best practices, pitfalls and opportunities,” IEEE Rev. Biomed. Eng., pp. 19-41, 2023, doi: https://doi.org/10.1109/RBME.2023.3331297
C. Cobelli, B. Kovatchev, “Developing the UVA/Padova Type 1 Diabetes Simulator: Modeling, Validation, Refinements, and Utility,” J. Diabetes Sci. Technol., vol. 17, no. 6, pp. 1493-1505, 2023, doi: https://doi.org/10.1177/19322968231195081
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Revista Mexicana de Ingenieria Biomedica

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Upon acceptance of an article in the RMIB, corresponding authors will be asked to fulfill and sign the copyright and the journal publishing agreement, which will allow the RMIB authorization to publish this document in any media without limitations and without any cost. Authors may reuse parts of the paper in other documents and reproduce part or all of it for their personal use as long as a bibliographic reference is made to the RMIB. However written permission of the Publisher is required for resale or distribution outside the corresponding author institution and for all other derivative works, including compilations and translations.







