Optimizing infection trajectories: Innovation in Controllability of Nonlinear SIR Model

Omar Zakary; Sara Bidah; Mostafa Rachik

doi:10.17488/RMIB.45.2.9

Authors

Omar Zakary Hassan II University of Casablanca, Faculty of sciences Ben M'Sik, Morocco https://orcid.org/0000-0003-0176-8233
Sara Bidah Hassan II University of Casablanca, Faculty of sciences Ben M'Sik, Morocco
Mostafa Rachik Hassan II University of Casablanca, Faculty of sciences Ben M'Sik, Morocco

DOI:

https://doi.org/10.17488/RMIB.45.2.9

Keywords:

controllability, control theory, infectious diseases, nonlinear models, SIR model

Abstract

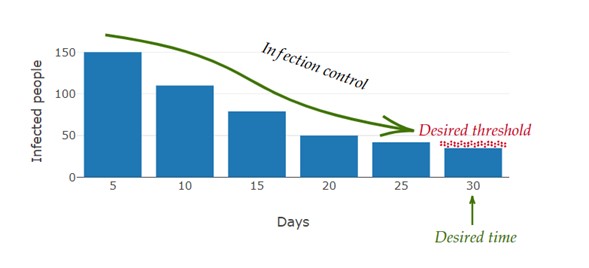
Managing infections within populations poses significant challenges, particularly in achieving controllability over nonlinear models within epidemiological systems. In this study, the challenge is addressed by introducing a novel control function tailored to enhance the management of infections. The approach revolves around leveraging a nonlinear SIR epidemiological model, enabling the derivation of explicit solutions and fine-tuning of control parameters to align with predefined objectives. Specifically, the focus lies on guiding the number of infected individuals towards a predetermined threshold at a specified time for all initial values. Through rigorous numerical simulations, the effectiveness of the proposed control strategy in achieving greater controllability and regulating the spread of infection over time is depicted, For example, our simulations show that starting with an initial infected population of 150 individuals in a population of 25,150, the control strategy can reduce the number of infected individuals to below 40 within 30 days. The quantitative results presented underscore the efficacy of the approach, highlighting its potential to significantly impact disease management strategies.

Downloads

Download data is not yet available.

References

J. Klamka, “Controllability of dynamical systems. a survey,” Bull. Pol. Acad. Sci. Tech. Sci., vol. 61, no. 2, pp. 335-342, 2013, doi: http://dx.doi.org/10.2478/bpasts-2013-0031

H. J. Sussmann and V. Jurdjevic, “Controllability of nonlinear systems,” J. Differ. Equ., vol. 12, no. 1, pp. 95-116, 1972, doi: http://dx.doi.org/10.1016/0022-0396(72)90007-1

L.-Z.Wang, R.-Q. Su, Z.-G. Huang, X.Wang, W.-X.Wang, C. Grebogi, and Y.-C. Lai, “A geometrical approach to control and controllability of nonlinear dynamical networks,” Nat. Commun., vol. 7, no. 1, 2016, art. no. 11323, doi:

http://dx.doi.org/10.1038/ncomms11323

R. Sakthivel, R. Ganesh, Y. Ren, and S. M. Anthoni, “Approximate controllability of nonlinear fractional dynamical systems,” Commun. Nonlinear Sci. Numer. Simul., vol. 18, no. 12, pp. 3498–3508, 2013, doi: http://dx.doi.org/10.1016/j.cnsns.2013.05.015

K. Beauchard and C. Laurent, “Local controllability of 1d linear and nonlinear schrödinger equations with bilinear control,” J. Math. Pures Appl., vol. 94, no. 5, pp. 520–554, 2010, doi: http://dx.doi.org/10.1016/j.matpur.2010.04.001

X.-L. Ding and J. J. Nieto Roig, “Controllability of nonlinear fractional delay dynamical systems with prescribed controls,” NAMC, vol. 23, no. 1, pp. 1-18, 2018, doi: http://dx.doi.org/10.15388/NA.2018.1.1

O. Zakary, A. Larrache, M. Rachik, and I. Elmouki, “Effect of awareness programs and travel-blocking operations in the control of hiv/aids outbreaks: a multi-domains sir model,” Adv. Differ. Equ., vol. 2016, no. 1, 2016, art. no. 169, doi:

http://dx.doi.org/10.1186/s13662-016-0900-9

O. Zakary, S. Bidah, M. Rachik, and H. Ferjouchia, “Mathematical model to estimate and predict the covid-19 infections in morocco: Optimal control strategy,” J. Appl. Math., vol. 2020, pp. 1–13, 2020, doi:

http://dx.doi.org/10.1155/2020/9813926

K. O. Kwok, A. Tang, V. W. Wei, W. H. Park, E. K. Yeoh, and S. Riley, “Epidemic models of contact tracing: systematic review of transmission studies of severe acute respiratory syndrome and middle east respiratory syndrome,” Comput. Struct. Biotechnol. J., vol. 17, pp. 186–194, 2019, doi: http://dx.doi.org/10.1016/j.csbj.2019.01.003

M. Moustafa, M. H. Mohd, A. I. Ismail, and F. A. Abdullah, “Dynamical analysis of a fractional-order ecoepidemiological model with disease in prey population,” Adv. Differ. Equ., vol. 2020, 2020, art. no. 48, doi:

https://doi.org/10.1186/s13662-020-2522-5

X. Wang, H. Peng, B. Shi, D. Jiang, S. Zhang, and B. Chen, “Optimal vaccination strategy of a constrained

time-varying seir epidemic model,” Commun. Nonlinear Sci. Numer. Simul., vol. 67, pp. 37–48, 2019, doi:

http://dx.doi.org/10.1016/j.cnsns.2018.07.003

P. C. Jentsch, M. Anand, and C. T. Bauch, “Prioritising covid-19 vaccination in changing social and epidemiological landscapes: a mathematical modelling study,” Lancet Infect. Dis., vol. 21, no. 8, pp. 1097–1106, 2021, doi:

http://dx.doi.org/10.1016/S1473-3099(21)00057-8

M. Lhous, O. Zakary, M. Rachik, E. M. Magri, and A. Tridane, “Optimal containment control strategy of the second phase of the covid-19 lockdown in morocco,” Appl. Sci., vol. 10, no. 21, 2020, art. no. 7559, doi:

http://dx.doi.org/10.3390/app10217559

Z. Omar, B. Sara, and R. Mostafa, “The impact of staying at home on controlling the spread of covid-19: Strategy of control,” Rev. Mex. Ing. Biomed., vol. 42, no. 1, 2021, doi: https://doi.org/10.17488/rmib.42.1.2

O. Zakary, M. Rachik, and I. Elmouki, “On the analysis of a multi-regions discrete sir epidemic model: an optimal control approach,” Int. J. Dynam. Control, vol. 5, pp. 917–930, 2017, doi: http://dx.doi.org/10.1007/s40435-016-0233-2

Z. Omar, M. Rachik, and I. Elmouki, “A new analysis of infection dynamics: multi-regions discrete epidemic model with an extended optimal control approach,” Int. J. Dynam. Control, vol. 5, pp. 1010–1019, 2017, doi:

http://dx.doi.org/10.1007/s40435-016-0264-8

D. Osthus, K. S. Hickmann, P. C. Caragea, D. Higdon, and S. Y. Del Valle, “Forecasting seasonal influenza with a state-space sir model,” Ann. Appl. Stat., vol. 11, no. 1, pp. 202-224, 2017, doi:

http://dx.doi.org/10.1214/16-AOAS1000

M. Kröger and R. Schlickeiser, “Analytical solution of the sir-model for the temporal evolution of epidemics. part a: time-independent reproduction factor,” J. Phys. A Math. Theor., vol. 53, 2020, art. no. 505601, doi:

http://dx.doi.org/10.1088/1751-8121/abc65d

C. Fraser, S. Riley, R. M. Anderson, and N. M. Ferguson, “Factors that make an infectious disease outbreak controllable,” Proc. Natl. Acad. Sci., vol. 101, no. 16, pp. 6146–6151, 2004, doi:

http://dx.doi.org/10.1073/pnas.0307506101

X. Zhao, K. Siegel, M. I.-C. Chen, and A. R. Cook, “Rethinking thresholds for serological evidence of influenza virus infection,” Influenza Other Respir. Viruses, vol. 11, no. 3, pp. 202–210, 2017, doi:

http://dx.doi.org/10.1111/irv.12452

F. D. Sahneh, F. N. Chowdhury, and C. M. Scoglio, “On the existence of a threshold for preventive behavioral responses to suppress epidemic spreading,” Sci. Rep., vol. 2, 2012, art. no. 632, doi:

http://dx.doi.org/10.1038/srep00632

F. Khondaker, “Optimal control analysis of Influenza epidemic model,” App. Math., vol. 13, no. 10, pp. 845-857, 2022, doi: https://doi.org/10.4236/am.2022.1310053

D. I. Ketcheson, “Optimal control of an SIR epidemic through finite-time non-pharmaceutical intervention,” J. Math. Biol., vol. 83, 2021, art. no. 7, doi: https://doi.org/10.1007/s00285-021-01628-9

L. Bolzoni, R. Della Marca, and M. Groppi, “On the optimal control of SIR model with Erlang-distributed infectious period: isolation strategies,” J. Math. Biol., vol. 83, 2021, art. no. 36, doi:

https://doi.org/10.1007/s00285-021-01668-1

E. V. Grigorieva, E. N. Khailov, and A. Korobeinikov. “Optimal control for a SIR epidemic model with nonlinear incidence rate,” Math. Model. Nat. Phenom., vol. 11, no. 4, pp. 89-104, 2016, doi:

https://doi.org/10.1051/mmnp/201611407

Fatmawati, C. W. Chukwu, R. T. Algahtani, C. Alfiniyah, F. F. Herdicho, Tasmi, “A pontryagin’s maximum principle and optimal control model with cost-effectiveness analysis of the COVID-19 epidemic,” Decis. Anal. J., vol. 8, 2023, art. no. 100273, doi: https://doi.org/10.1016/j.dajour.2023.100273