Optimizing infection trajectories: Innovation in Controllability of Nonlinear SIR Model
DOI:
https://doi.org/10.17488/RMIB.45.2.9Palabras clave:
controllability, control theory, infectious diseases, nonlinear models, SIR modelResumen
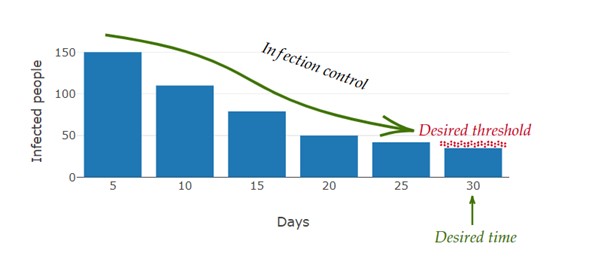
Managing infections within populations poses significant challenges, particularly in achieving controllability over nonlinear models within epidemiological systems. In this study, the challenge is addressed by introducing a novel control function tailored to enhance the management of infections. The approach revolves around leveraging a nonlinear SIR epidemiological model, enabling the derivation of explicit solutions and fine-tuning of control parameters to align with predefined objectives. Specifically, the focus lies on guiding the number of infected individuals towards a predetermined threshold at a specified time for all initial values. Through rigorous numerical simulations, the effectiveness of the proposed control strategy in achieving greater controllability and regulating the spread of infection over time is depicted, For example, our simulations show that starting with an initial infected population of 150 individuals in a population of 25,150, the control strategy can reduce the number of infected individuals to below 40 within 30 days. The quantitative results presented underscore the efficacy of the approach, highlighting its potential to significantly impact disease management strategies.
Descargas
Citas
J. Klamka, “Controllability of dynamical systems. a survey,” Bull. Pol. Acad. Sci. Tech. Sci., vol. 61, no. 2, pp. 335-342, 2013, doi: http://dx.doi.org/10.2478/bpasts-2013-0031
H. J. Sussmann and V. Jurdjevic, “Controllability of nonlinear systems,” J. Differ. Equ., vol. 12, no. 1, pp. 95-116, 1972, doi: http://dx.doi.org/10.1016/0022-0396(72)90007-1
L.-Z.Wang, R.-Q. Su, Z.-G. Huang, X.Wang, W.-X.Wang, C. Grebogi, and Y.-C. Lai, “A geometrical approach to control and controllability of nonlinear dynamical networks,” Nat. Commun., vol. 7, no. 1, 2016, art. no. 11323, doi:
http://dx.doi.org/10.1038/ncomms11323
R. Sakthivel, R. Ganesh, Y. Ren, and S. M. Anthoni, “Approximate controllability of nonlinear fractional dynamical systems,” Commun. Nonlinear Sci. Numer. Simul., vol. 18, no. 12, pp. 3498–3508, 2013, doi: http://dx.doi.org/10.1016/j.cnsns.2013.05.015
K. Beauchard and C. Laurent, “Local controllability of 1d linear and nonlinear schrödinger equations with bilinear control,” J. Math. Pures Appl., vol. 94, no. 5, pp. 520–554, 2010, doi: http://dx.doi.org/10.1016/j.matpur.2010.04.001
X.-L. Ding and J. J. Nieto Roig, “Controllability of nonlinear fractional delay dynamical systems with prescribed controls,” NAMC, vol. 23, no. 1, pp. 1-18, 2018, doi: http://dx.doi.org/10.15388/NA.2018.1.1
O. Zakary, A. Larrache, M. Rachik, and I. Elmouki, “Effect of awareness programs and travel-blocking operations in the control of hiv/aids outbreaks: a multi-domains sir model,” Adv. Differ. Equ., vol. 2016, no. 1, 2016, art. no. 169, doi:
http://dx.doi.org/10.1186/s13662-016-0900-9
O. Zakary, S. Bidah, M. Rachik, and H. Ferjouchia, “Mathematical model to estimate and predict the covid-19 infections in morocco: Optimal control strategy,” J. Appl. Math., vol. 2020, pp. 1–13, 2020, doi:
http://dx.doi.org/10.1155/2020/9813926
K. O. Kwok, A. Tang, V. W. Wei, W. H. Park, E. K. Yeoh, and S. Riley, “Epidemic models of contact tracing: systematic review of transmission studies of severe acute respiratory syndrome and middle east respiratory syndrome,” Comput. Struct. Biotechnol. J., vol. 17, pp. 186–194, 2019, doi: http://dx.doi.org/10.1016/j.csbj.2019.01.003
M. Moustafa, M. H. Mohd, A. I. Ismail, and F. A. Abdullah, “Dynamical analysis of a fractional-order ecoepidemiological model with disease in prey population,” Adv. Differ. Equ., vol. 2020, 2020, art. no. 48, doi:
https://doi.org/10.1186/s13662-020-2522-5
X. Wang, H. Peng, B. Shi, D. Jiang, S. Zhang, and B. Chen, “Optimal vaccination strategy of a constrained
time-varying seir epidemic model,” Commun. Nonlinear Sci. Numer. Simul., vol. 67, pp. 37–48, 2019, doi:
http://dx.doi.org/10.1016/j.cnsns.2018.07.003
P. C. Jentsch, M. Anand, and C. T. Bauch, “Prioritising covid-19 vaccination in changing social and epidemiological landscapes: a mathematical modelling study,” Lancet Infect. Dis., vol. 21, no. 8, pp. 1097–1106, 2021, doi:
http://dx.doi.org/10.1016/S1473-3099(21)00057-8
M. Lhous, O. Zakary, M. Rachik, E. M. Magri, and A. Tridane, “Optimal containment control strategy of the second phase of the covid-19 lockdown in morocco,” Appl. Sci., vol. 10, no. 21, 2020, art. no. 7559, doi:
http://dx.doi.org/10.3390/app10217559
Z. Omar, B. Sara, and R. Mostafa, “The impact of staying at home on controlling the spread of covid-19: Strategy of control,” Rev. Mex. Ing. Biomed., vol. 42, no. 1, 2021, doi: https://doi.org/10.17488/rmib.42.1.2
O. Zakary, M. Rachik, and I. Elmouki, “On the analysis of a multi-regions discrete sir epidemic model: an optimal control approach,” Int. J. Dynam. Control, vol. 5, pp. 917–930, 2017, doi: http://dx.doi.org/10.1007/s40435-016-0233-2
Z. Omar, M. Rachik, and I. Elmouki, “A new analysis of infection dynamics: multi-regions discrete epidemic model with an extended optimal control approach,” Int. J. Dynam. Control, vol. 5, pp. 1010–1019, 2017, doi:
http://dx.doi.org/10.1007/s40435-016-0264-8
D. Osthus, K. S. Hickmann, P. C. Caragea, D. Higdon, and S. Y. Del Valle, “Forecasting seasonal influenza with a state-space sir model,” Ann. Appl. Stat., vol. 11, no. 1, pp. 202-224, 2017, doi:
http://dx.doi.org/10.1214/16-AOAS1000
M. Kröger and R. Schlickeiser, “Analytical solution of the sir-model for the temporal evolution of epidemics. part a: time-independent reproduction factor,” J. Phys. A Math. Theor., vol. 53, 2020, art. no. 505601, doi:
http://dx.doi.org/10.1088/1751-8121/abc65d
C. Fraser, S. Riley, R. M. Anderson, and N. M. Ferguson, “Factors that make an infectious disease outbreak controllable,” Proc. Natl. Acad. Sci., vol. 101, no. 16, pp. 6146–6151, 2004, doi:
http://dx.doi.org/10.1073/pnas.0307506101
X. Zhao, K. Siegel, M. I.-C. Chen, and A. R. Cook, “Rethinking thresholds for serological evidence of influenza virus infection,” Influenza Other Respir. Viruses, vol. 11, no. 3, pp. 202–210, 2017, doi:
http://dx.doi.org/10.1111/irv.12452
F. D. Sahneh, F. N. Chowdhury, and C. M. Scoglio, “On the existence of a threshold for preventive behavioral responses to suppress epidemic spreading,” Sci. Rep., vol. 2, 2012, art. no. 632, doi:
http://dx.doi.org/10.1038/srep00632
F. Khondaker, “Optimal control analysis of Influenza epidemic model,” App. Math., vol. 13, no. 10, pp. 845-857, 2022, doi: https://doi.org/10.4236/am.2022.1310053
D. I. Ketcheson, “Optimal control of an SIR epidemic through finite-time non-pharmaceutical intervention,” J. Math. Biol., vol. 83, 2021, art. no. 7, doi: https://doi.org/10.1007/s00285-021-01628-9
L. Bolzoni, R. Della Marca, and M. Groppi, “On the optimal control of SIR model with Erlang-distributed infectious period: isolation strategies,” J. Math. Biol., vol. 83, 2021, art. no. 36, doi:
https://doi.org/10.1007/s00285-021-01668-1
E. V. Grigorieva, E. N. Khailov, and A. Korobeinikov. “Optimal control for a SIR epidemic model with nonlinear incidence rate,” Math. Model. Nat. Phenom., vol. 11, no. 4, pp. 89-104, 2016, doi:
https://doi.org/10.1051/mmnp/201611407
Fatmawati, C. W. Chukwu, R. T. Algahtani, C. Alfiniyah, F. F. Herdicho, Tasmi, “A pontryagin’s maximum principle and optimal control model with cost-effectiveness analysis of the COVID-19 epidemic,” Decis. Anal. J., vol. 8, 2023, art. no. 100273, doi: https://doi.org/10.1016/j.dajour.2023.100273
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2024 Omar Zakary, Sara Bidah, Mostafa Rachik

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.
Una vez que el artículo es aceptado para su publicación en la RMIB, se les solicitará al autor principal o de correspondencia que revisen y firman las cartas de cesión de derechos correspondientes para llevar a cabo la autorización para la publicación del artículo. En dicho documento se autoriza a la RMIB a publicar, en cualquier medio sin limitaciones y sin ningún costo. Los autores pueden reutilizar partes del artículo en otros documentos y reproducir parte o la totalidad para su uso personal siempre que se haga referencia bibliográfica al RMIB. No obstante, todo tipo de publicación fuera de las publicaciones académicas del autor correspondiente o para otro tipo de trabajos derivados y publicados necesitaran de un permiso escrito de la RMIB.











